UNDER CONSTRUCTION

REAL EXAMPLE OF ELECTRONS FED BACK WITH GRADUALLY INCREASING ENERGY TO INFINITI

OR THEY DESTROY THE  SET UP OF THE APPARATUS BEYOND A CERTAIN AMOUNT OF THE CREATED ENERGY

ΠΑΡΑΔΕΙΓΜΑ ΑΝΑΤΡΟΦΟΔΟΤΗΣΗΣ ΗΛΕΚΤΡΟΝΙΩΝ ΤΩΝ ΟΠΟΙΩΝ Η ΕΝΕΡΓΕΙΑ ΘΑ ΑΠΕΙΡΙΖΕΤΑΙ

Η ΘΑ ΔΗΜΙΟΥΡΓΟΥΝ ΑΥΤΟΚΑΤΑΣΤΡΟΦΗ ΤΗΣ ΣΥΣΚΕΥΗΣ ΠΕΡΑ ΑΠΟ ΕΝΑ ΠΟΣΟ ΔΗΜΙΟΥΡΓΗΘΗΣΗΣ ΕΝΕΡΓΕΙΣ, ΣΥΜΦΩΝΑ ΜΕ ΤΗΝ ΣΧΕΤΙΚΗ ΘΕΩΡΕΙΑ ΑΕΙΚΙΝΗΤΩΝ, βλέπετε παρακάτω

ΑΝΑΛΥΣΙΣ

 Στοιχεία Φυσικής
Με κατάλληλο Μαγνητικα Πεδία Η, Όπως δείχνει το  σχήμα παρακάτω και παραπάνω.

Σχ. 1. Ή διεύθυνσις του μαγνητικού πεδίου είναι κάθετος επί το επίπεδο του σχήματος.

Ο πόλος του μαγνήτη έχει τετραγωνική μορφή.

Ηλεκτρόνιο κινούμενο εντός του μαγνητικού πεδίου  (σχ. 1), υφίσταται μίαν δύναμιν κατά Laplace F, ίση προς

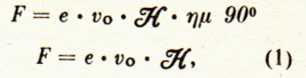
η οποία κατά την Μηχανική, προκαλεί καμπύλωση της τροχιάς.Την μορφή της τροχιάς του ηλεκτρονίου εντός του μαγνητικού πεδίου ευρίσκουμε ώς εξής : Ώς γνωστόν ή δύναμις κατά Laplace F είναι κάθετος επί τό επίπεδο των ανυσμάτων u₀ και H, συνεπώς είναι διαρκώς κάθετος επί την ταχύτητα u₀  Άρα, ή δύναμις αυτή προκαλεί κεντρομόλο, μόνο, επιτάχυνση γ_κ, η οποία ως γνωστόν είναι ίση προς: 

                (2)

Επειδή κατά την εξίσωση (1), ή δύναμις F είναι σταθερά, έπεται ότι καί ή κεντρομόλος επιτάχυνση γ_κ θά είναι σταθερά. Τούτο σημαίνει, κατά τόν τύπον (2), ότι και ή άκτίς r θά είναι σταθερά, οπότε ή τροχιά θα είναι κύκλος (ή τόξον κύκλου). Ή άκτίς r τής κυκλικής τροχιάς υπολογίζεται εκ του Θεμελιώδους νόμου της Μηχανικής:

Λύοντες ως προς r και Η λαμβάνουμε τις σχέσεις:

Παρατήρηση: Εφόσον ή έπί του ηλεκτρονίου εξασκούμενη δύναμις είναι διαρκώς κάθετος επί την ταχύτητα, έπεται ότι το μέτρο της ταχύτητος θά παραμένει σταθερό. Τούτο  σημαίνει ότι   το   μαγνητικό  πεδίον ούτε δίδει, ούτε  αφαιρεί  ενέργεια   εκ του  κινουμένου   ηλεκτρονίου.

=========================================

ΗΛΕΚΤΡΟΠΑΡΑΓΩΓΟ ΖΕΥΓΟΣ ΜΕ ΑΝΑΤΡΦΟΔΟΤΗΣΗ ΤΗΣ
 ΕΞΟΔΟΥ

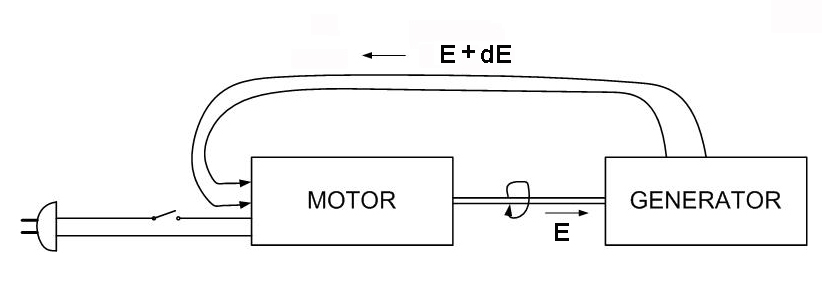
Η ποσότης dE  που υπολείπεται ή πλεονάζει από την Γεννητρια σε χρόνο dt είναι ανάλογος της ολικής ενεργείας διέγερσης Ε αυτής της Γεννητρίας, δηλαδή στα 100  Ε διέγερσης, το dE είναι 5, ας πούμε, στα 200 Ε διέγερσης το dE είναι 10, δηλαδή

dE / dt = kE. Αυτή η σχέσης είναι μία ομογενής διαφορική  γραμμική εξίσωση, πρώτης τάξεως.  Η γενική της λύση είναι

Ε = Ε_{0 e}^kt.

^{Διακρίνομε τις εξης τρείς περιπτωσεις 1) Κ<0, 2) Κ=0, 3) Κ>0 , με τον διακόπτη εξωτερικής τροφοδοσίας κλειστό.}

   _{1) Αν Κ<0, τότε το Ε φθίνει και το ηλεκτροπαραγωγό σύστημα κάποτε σταματά, όταν  το Ε γίνει μηδέν, Ε =0}

2) Αν Κ =0 τό σύστημα έχει σταθερά ενέργεια και το σύστημα θα κινείται, επαόριστον, δηλαδή το σύστημα θα είναι αεικινητόν.. Η περίπτωση είναι εξαιρετικά απιθανως, όσο η πιθανότατης γιά το Κ νά είναι μηδέν, από το σύνολο των θετικών και αρνητικών αριθμών, δηλαδή η πιθανοτης στή πραγματκότητα είναι μηδέν

3) Αν Κ>0, η ενέργεια Ε του συστήματος απειρίζεται, και το σύστημα αυτοκαταστρέφεται

Αυτή  η τρίτη περίπτωση είναι η πιο συνηθισμένη περίπτωση γιά τα αεικίνητα.