Click here for
E = kmc2
partial translation
in English![]()
DISREGARD
E=m c2
TO FREE SCIENCE, BIOLOGY AND MEDICINE
ΔΙΕΘΝΗΣ ΠΡΟΣΦΟΡΑ ΔΙΑΡΚΕΙΑΣ ΑΠΟ 30/09/2006
100.000 (ΕΚΑΤΟ
ΧΙΛΙΑΔΕΣ) ΕΥΡΩ ή ΔΥΟ ΣΥΣΚΕΥΈΣ
PAPIMI, ΣΕ ΟΠΟΙΟΝ ΔΙΑΨΕΥΣΕΙ ΤΗΝ
ΒΑΣΙΚΗ ΜΑΣ ΘΕΣΗ ΕΔΩ
"Η σχέση μάζης ενέργειας
του Einstein
Ε = MC2
Δεν Ισχύει Γενικώς"
ισοδύναμα
"Ο τύπος του
Einstein
Ε = MC2
Δεν ειναι η ορθή έκφραση για την σχέση μάζης ενέργειας"
Πρώτη Δημοσίευση 10/06/2005.
Συμπλήρωση 15/06/2005, 19/06/2005
Διόρθωση 17/06/2005, 18/06/2005
ΟΡΓΑΝΩΣΗ
Ένωση Ελλήνων Φυσικών & ΤΕΙ ΠΕΙΡΑΙΩΣ
Β' ΠΑΡΟΥΣΙΑΣΗ
Παρασκευή 1/7/2005, 8μμ, Μεγ. Αμφιθεατρο Χατζηνικολαου
Π. Ράλλη και Θηβών 255, TEI ΠΕΙΡΑΙΩΣ
Εισαγωγή, Περίληψη, Συμπεράσματα,
Ευρεία Συζήτηση-Ευκαιρία Κριτικής
ΠΡΑΓΜΑΤΟΠΟΙΗΘΗΚΕ ΜΕ ΜΕΓΑΛΗ ΠΛΗΡΟΤΗΤΑ
Δεν διατυπώθηκε καμία κριτική ή παρατήρηση ενάντια
στο
παρόν περιεχόμενο,είτε διά ζώσης, είτε ηλεκτρονικά,
είτε διά κάποιου άλλου τρόπου.
Γιά άμεση κριτική,
συζήτηση, δημοσίευση:
![]()
![]()
info@papimi.gr isnot functional
www.papimi.gr
click
HELLENIC VERSION
Ε0 = ΚM0
ΠΑΝΑΓΙΩΤΟΥ ΠΑΠΠΑ
Η περίφημη εξίσωση
Ε = MC2
προσφέρει τα
ελάχιστα σε σχέσει
με την συσκότιση της γνώσης και της επιστήμης, με την αφαίμαξη και την
στραγγαλισμό βασικών
επιστημονικών τομέων, όπως της:
Υγείας
Βιολογίας
Ιατρικής
Φυσιολογίας
Φυτολογίας
Πυρηνικής
Ψυχρής πυρηνικής σύντηξης
Χημείας
Αλχημείας
Γεωλογίας
Κοσμολογίας
Πυρηνικής τεχνολογίας
Τεχνολογίας υλικών
και αμέτρητων άλλων τομέων
που δεν αναφέρουμε εδώ.
Ο ΦΑΥΛΟΣ ΚΥΚΛΟΣ ΤΗΣ ΕΝΕΡΓΕΙΑΣ ΚΑΙ ΟΡΜΗΣ ΤΩΝ ΦΩΤΟΝΙΩΝ
Στην μοντέρνα φυσική το φώς θεωρείται ότι
αποτελείται από φωτόνια. Τα φωτόνια θεωρούνται ταυτόχρονα σαν σωμάτια με μάζα,
ενέργεια και ορμή και σαν κύμα με μήκος κύματος, συχνότητα και ταχύτητα.
Σύμφωνα με την κλασσική φυσική, η ενέργεια των φωτονίων σαν σωμάτια θα έπρεπε να
ήταν Ε= (1/2)mC2,
όπου C
η ταχυτητα τους, από τόν γνωστό νόμο του Νευτονα. Επίσης, κλασσικά, η ορμή τους
είναι P=mc
και επομένως
Ε = (1/2)mC2
= (1/2)mCC
= (1/2)PC.
(1)
Εντούτοις γιά τα φωτόνία στην μοντέρνα φυσική, η σχέση μεταξύ ενέργειας Ε και
ορμής των P,
υποθέτουμε ότι ειναι:
E = PC (2)
H
καλύτερη (ή, κυρίως, η εκτενέστερη) πειραματική επιβεβαίωση της μοντέρνας
υπόθεσης αυτής είναι μάλλον έμμεση. Προέρχεται από την πυρηνική φυσική και τα
στοιχειώδη σωμάτια, όπου δεχόμαστε ότι η ανάλυση των κρούσεων φωτονίων και άλλων
σωματιδίων γίνεται μέσω της ισχύος της παραπάνω εξίσωσης(2).
Tα
μόνα πειράματα με σκοπό την εξέταση της σχέσης ενέργειας και ορμής των φωτονίων
έγιναν με συνεχείς δέσμες φωτός, και όχι με φωτόνια, με σκοπό τη μελέτη του
φαινομένου ακτινοβολίας - πίεσης.
Tέτοια
πειράματα περιλαμβάνουν πτώση μεγάλου πλήθους φωτονίων (π.χ. 1
Watt
ορατού φωτός αντιπροσωπεύει ροή 3X1018
φωτονίων/sec
περίπου) και είναι δυνατόν μόνο να
περιγραφούν και να αναλυθούν σε συνάρτηση με τη ροή ακτινοβόλου ενέργειας, χωρίς
την παραπομπή στη φωτονική κατασκευή της ακτινοβολίας. Πράγματι, είναι
γεγονός ότι η εξίσωση (2), ως γενική διατύπωση της σχέσης ενέργειας και ορμής
της ακτινοβολίας στο κενό, ήταν παραδεκτή ευρέως πριν από την ανακάλυψη της
κβαντικής συμπεριφοράς της, Εφ’
όσον ήταν αναγκαίο επακόλουθο της
ηλεκτρομαγνητικής θεωρίας του
Maxwell
- Ομως η θεωρία αυτή, η οποία έδωσε την ορθή τιμή στην ταχύτητα του φωτός από τη
φυσική των βασικών ηλεκτρικών και μαγνητικών φαινομένων, δεν
κατοχυρώνεται και δεν εξουσιοδοτείται γιά το γεγονός αυτό και μόνο (του
προσδιορισμού του C), να υπαγορεύει την αλήθεια επί
παντός άλλου θέματος χωρίς απόδειξη.
Το κατπληκτικό είναι, τα
πειράματα για την απόδειξη της ακτινοβολίας - πίεσης,
αντίθετα έγιναν αρχικά σαν απόπειρα επιβεβαίωσης της
θεωρίας του Maxwell.
Mε
δεδομένη δε τη φωτονική εικόνα (σωματιδιακή), υποτέθηκε ότι η εξίσωση (2)
θα έπρεπε να ισχύει
επίσης και για ένα φωτόνιο-σωμάτιο.
Πραγματικά, όλα τα πειράματα
ακτινοβολίας - πίεσης είναι βασικά όμοια. Συνίστανται στη μέτρηση της δύναμης
F,
την οποία μία ροή (γνωστή από την προσπίπτουσα ισχύ
W)
ακτινοβόλου ενέργειας εξασκεί πάνω σε μία επιφάνεια.
H
εξεταζόμενη επιφάνεια είναι μία λεπτή
μεταλλική πτέρυγα /πλάκα αναρτημένη πάνω σε ένα λεπτό νήμα στρέψης.
H
ενέργεια της ροής μετριέται από το
αποτέλεσμα της θερμότητας(!). Λαμβάνεται υπ’ όψη ο λόγος ρ της προσπίπτουσας
ακτινοβολίας προς αυτήν που ανακλάται από το φύλλο, εφ’ όσον το φως
που ανακλάται συνεισφέρει στη δύναμη της
ακτινοβολίας. Mία
επιφάνεια τέλειας ανάκλασης θα υφίσταται διπλάσια δύναμη από εκείνη που
υφίσταται μία επιφάνεια τέλειας απορρόφησης, για την ίδια προσπίπτουσα ροή
ακτινοβολίας. Αυτή είναι η αρχή του ραδιομέτρου που αποτελείται από ένα
οριζόντιο μήλο από κατακόρυφα φύλα, που κατά την μία όψη
τα φύλα αυτά θεωρούνται τελείως απορροφητικά και κατά την άλλη όψη τελείως
ανακλαστικά. Τα φύλα τοποθετούνται με όμοιο τρόπο (βλεπετε σχήμα)

Φωτ. 1 Ραδιομέτρου. Το Ραδιόμετρο περιστρέφεται ανάποδα
στη πρόσπτωση του φωτός, σαν το φώς να έχει αντίθετη ορμή - P,
από ότι πιστεύεται.
Το Ραδιόμετρο ανακαλύφθηκε από τον διάσημο Crookes
(Θυμηθείτε τις Ακτίνες Crooke's). Ο Crookes
είχε ανακαλύψει και πολλές άλλες ανωμαλίες του Ραδιομέτρου. οι
οποίες τώρα φαίνονται να ξεχάσθηκαν. Σύντομα θα επανέλθωμεν.
έτσι ώστε όλες οι ανακλαστικές επιφάνειες να προσφέρουν μία πχ δεξιόστροφο ροπή στέψεως, ενώ όλες οι απορροφητικές επιφάνειες να προσφέρουν πχ μία αριστερόστροφη στρέψη. Επειδή, τώρα η δύναμη πάνω στην ανακλαστική επιφάνεια είναι διπλασία από την δύναμη πάνω στη εκάστοτε απορροφητική επιφάνεια, θα υπερισχύει η στρέψη των ανακλαστικών επιφανειών από την πίεση των φωτονίων. ΕΝΤΟΥΤΟΙΣ ΣΕ ΟΛΑ ΤΑ ΡΑΔΙΟΜΕΤΡΑ ΠΑΡΑΤΗΡΕΙΤΑΙ ΤΟ ΑΝΤΙΘΕΤΟ: ΥΠΕΡΙΣΧΥΕΙ Η ΠΙΕΣΗ ΤΩΝ ΑΠΟΡΡΟΦΗΤΙΚΩΝ ΕΠΙΦΑΝΕΙΩΝ. Τούτο το παράδοξο δικαιολογείται λέγοντας, πραγματικά η πίεση των φωτονίων είναι πάρα πολύ μικρά και δεν παρατηρείται. Παρατηρείται όμως, η πίεση ανακλωμένων σωματιδίων από τις θερμαινόμενες απορροφητικές επιφάνειες, λόγω της ύπαρξης άλλων παρασιτικών σωματιδίων, από το ατελές κενό του ραδιομέτρου. Ειναι γνωστό ότι το τέλειο κενό δεν έχει επιτευχθεί ακόμη.
Από τα πειράματα συσχέτισης ακτινοβολίας και
πίεσης που αναφέρονται, συνηθέστερα είναι εκείνα των
Nichols
και
Hull
[5]. Oι
μετρήσεις τους ήταν πολύ προσεκτικές και επιδέξιες, τα δε αποτελέσματά τους
υποτίθεναι ότι επαλήθευσαν την εξίσωση (2) καλύτερα από 1%, [?]. Όμως οι
εργασίες τους αυτές έγιναν πριν την επίτευξη υψηλού κενού σε εργαστηριακό
επίπεδο και γι’ αυτό το λόγο τα αποτελάσματα τους, σωστά
δεν μπορούν ισχύουν με την δοθείσα ακρίβεια, Διότι δεν έκαναν
τον διαχωρισμό της αληθινής πίεσης της ακτινοβολίας από τη νόθο πίεση του
φαινομένου του ραδιόμετρου, που το κάνει να στρέφεται ανάποδα. Κατά συνέπεια δεν
υπήρξε άμεση πειραματική επαλήθευση της ακριβούς ποσοτικής σχέσεως της ενέργειας
και ορμής των φωτονίων:
E =
PC
=
mC2,
Στην παρούσα παρουσίαση θα δανεισθούμε την υπόθεση ότι ισχύει ο τύπος E = PC = mC2 ή γενικότερα =ΚmC2, για τα φωτόνια, με Κ κοντα στο 1 ή ακόμη Κ οτιδήποτε απο μαθηματικής πλευράς. Θα αποδείξουμε ότι o AE δεν έδωσε (ορθές) μαθηματικές αποδείξεις της περίφημης ισοδυναμίας μάζης και ενέργειας γιά τον τύπο E=mc2 γενικότερα για τυχόν σώμα μάζης m.
Ο τυπος αυτος ηταν θεωρητικα γνωστος απο τον ηλεκτρομαγνητισμο του
Maxwell, απο τον τυπο Ε=pc=mcc. Ο ΑΕ
θέλησε να του δωσει γενική ισχυ για όλα τα σωματα χωρις να πετυχει την γενική
του αποδειξη, όπως θα δούμε. Σήμερα ο τύπος αυτος αποδιδεται στον ΑΕ. Ο τύπος
αυτός θεωρείται απο τα σχολικά βιβλία σαν τον μεγαλυτερο τύπο της φυσικής και
την μεγαλύτερη κατακτηση του ανθρωπινου πνευματος στη φυσική σημερα! Εντούτοις,
η αυστηρη μαθηματικη (ποσοτικη) εφαρμογή του τύπου αυτου σημερα περιοριζει την
θεωρητική δυνατοτητα πολλων φυσικων φαινομενων απο το να πραγματοποιούνται, όπως
της ψυχρης πυρηνικής συντηξης, των πυρηνικων βιολογικών αντιδρασεων με τεραστια
εφαρμογή στην βιολογια, ιατρική και υγεια, την παραγωγη πολυτίμων μεταλλων και
πολυτιμων υλών κ.α. Θα λέγαμε ο τύπος αυτός πολύ περισσότερο και
δυσανάλογα περιορίζει την γνωση και την επιστημη παρά προσφερει σε αυτές.
Ο τύπος αυτός πρωτοδοθηκε απο τον ΑΕ σαν σταθερά ολοκληρώσεως βραδέως
επιταχυνομένων ηλεκτρονίων, (slowly accelerated electrons,
βλεπετε παρακατω, κεφάλαιο 10, απο τις εκδοσεις Dover
αναπαραγώμενο πρωτότυπο), προφανως παρασυρόμενος από την προηγούμενη μονογραφία
του Lorentz στον Ηλεκτρομαγνητισμό, με ταυτόσημο τίτλο-
θέμα. (Αντιπαράβαλε τις φωτοτυπίες των τίτλων των δυο εργασιών παρακατω).
Εντούτοις ο τύπος αυτός μπορει να δωθει πιό γενικά και πιό απλα σαν αυθαίρετη
σταθερά ολοκληρώσεως στα πλαίσια τόσο της Κλασσικής Μηχανικής του Νεύτωνα, όσο
και στα πλαίσια της "Μοντέρνας" Μηχανικής. Βλέπετε παρακάτω αποδείξεις Α' και
Β'.
Στην συνέχεια δίδουμε δύο αποδείξεις για την αναγκαιότητα κάποιας ισοδυναμίας
μάζης και ενέργειας τόσο στα πλαίσια της Κλασσικής Μηχανικης του Νεύτωνα, όσο
και στα πλαίσια της Μοντερνας Μηχανικής, με ταυτόσημο τρόπο, καταδεικνύοντας
έτσι, αντίθετα απο τι λέγεται, ότι για την κάποια ισοδυναμία μάζης και
ενέργειας, ειναι μύθος το γεγονος ότι αυτή είναι αποκλειστικό προνόμιο της
Σχετικότητας του ΑΕ. Η κάποια ισοδυναμια (προς το παρόν ακόμη άγνωστος στις
λεπτομέρειες της), ειναι εξ' ισου αποτέλεσμα και προνόμοιο της Κλασσικής
Μηχανικής. Τέλος δίδουμε δύο ακόμη μετέπειτα απόπειρες ανεπιτυχών αποδείξεων του
ΑΕ γιά τον υποτιθέμενο περίφημο τύπο του. Μία ακόμη του 1905, που ξεκινά με ένα
λάθος φαινόμενο Doppler και εντούτοις αυστηρά καταλήγει,
οχι στόν τύπο E=mc2, αλλά γενικότερα στον τύπο
E=κmc2, με κ οτιδήποτε.
Και μία τρίτη απόπειρα απόδειξης του 1906, που και αυτή αυθαιρετεί για να καταλήξει στον
τύπο E=mc2.
Ειρωνικά, η χρήση της ορμής κατά την κλασσική μηχανική, καταλήγει στον απροσδόκητο τύπο
E=(1/2)mc2.
Πιστεύουμε ότι η ορθή σχέση ισοδυναμίας μάζης και ενέργειας δεν είναι ενιαία για όλες τις περιπτώσεις, λεπτομέρειες της οποίας μένουν να ευρεθούν για το καλό της Ανθρωπότητας.
Α' ΑΠΟΔΕΙΞΗ ΠΠ
Με το Θεώρημα Κινητικής Ενέργειας
Κλασσικά
Έστω μια δύναμης F δρα σε
ένα σώμα και το επιταχύνει με επιτάχυνση γ, τότε ισχύουν
τα εξής:
F = mγ = mdu/dt =dp/dt
Ενέργεια =
ΑΠΟΔΕΙΞΗ ΑΕ ΓΙΑ ΤΗΝ ΚΙΝΗΤΙΚΗ ΕΝΕΡΓΕΙΑ
ΑΠΟ ΤΟ ΠΡΩΤΟΤΥΠΟ
(Παρακάτω αντιπαραθέτουμε το πρωτότυπο από τις εκδόσεις Dover, "The Principle of Relativity", σελίδες 9, 35, 61-63, Standard Book # 486-60081-5.)

Φωτ. 2 με το εξώφυλλο της έκδοσης Dover 1952

Φωτ. 3 και 4 με παρόμοιους τίτλους και περιεχόμενο της δημοσιεύσεως Lorentz 1904 και της δημοσίευσης Einstein 1905.

Φωτ. 5, έκδοσης Dover σελ. 61 που επιχειρείται να δοθεί απόδειξη για το Ε=mc
2 στά πλαίσια του ηλεκτρομαγνητισμού (ηλεκτρόνιο) κατά την πρακτική του Λορεντζ, παρότι η επιχειρούμενη απόδειξη εύκολα γενεκεύεται και απλοποιείται σε κάθε περίπτωση με το θεώρημα κινητικής ενεργείας.

Φωτ. 6, έκδοσης Dover σελ. 62, οπού οι περίεργες εξισώσεις δεν είναι τίποτα άλλο από τον θεμελιώδη νόμο του Νεύτωνα.

Φωτ. 7, έκδοσης Dover σελ. 63, όπου τα ολοκληρώματα δεν είναι τίποτα άλλο τα ολοκληρώματα έργου δυνάμεως. (τελικά τα ολοκληρώματα μεταπηδάνε σε ορισμένα ολοκληρώματα- ας πούμε ένα μικρό λάθος).
Β' ΑΠΟΔΕΙΞΗ ΠΠ
Μοντέρνα Αναπαραγωγή χρησιμοποιώντας το πρωτότυπο του ΑΕ,
ακριβώς στα ιδια πλαισια, οπως και στην κλασσικη Μηχανική του Νευτωνα, με το
θεωρημα της κινητικής ενεργειας δυνάμεως,
με πολύ πιο απλό τρόπο.
Θεώρημα Κινητικής Ενέργειας Μοντέρνα
Έστω μια δύναμης F δρα σε
ένα σώμα και το επιταχύνει, τότε ισχύουν τα εξής:
F =dp/dt = d(mu)/dt
m =m0/(1-u2/c2)1/2
Ενέργεια =
m0
⌠u/(1-u2/c2)3/2 )du =Γ' ΑΠΟΔΕΙΞΗ ΠΠ
ΓΙΑ ΤΗΝ ΑΝΑΓΚΑΙΟΤΗΤΑ ΔΥΝΑΜΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΜΑΖΗΣ - ΚΛΑΣΣΙΚΑ
Πρωτότυπη απόδειξη αναγκαιότητας
συνάρτησης ισοδυναμίας μαζης και ενέργειας στα πλαίσια της Κλασσικής Μηχανικής
από τον ΠΠ.
Έστω ένα σώμα, εν ηρεμία, με ολική ενέργεια
Ε0, απορροφά ένα φωτόνιο με ενέργεια Εφ = PC.
Και έστω μετά την απορρόφηση το σώμα αποκτά ενέργεια Ε1,
τότε ισχύουν τα εξής:
Εφ = PC = hv
E0= Δυναμική + Θερμική + κλπ
(Σε παρένθεση μπορούμε να πούμε ότι το Ε0
είναι η σταθερά ολοκλήρωσης του ολοκληρώματος του θεωρήματος της κινητικής
ενέργειας)
P0 =0, M0,
αρχική ορμή και μάζα του σώματος πριν την απορρόφηση του φωτονίου.
u απόκτηση κάποιας ταχύτητας για το σώμα μετά την
απορρόφηση του φωτονίου.
Θα είναι
E1 = E0 + 1/2Pu, E1 = E0 +
PC, άρα
1/2u=C,
u =2C. Άτοπο, διότι:
M0u = hv/C,
u = hv/(M0C)
Αναγκαστικά πρέπει να πούμε ότι, μετά την
αλληλεπίδραση, έχουμε ένα νέο σώμα, μέ νέα σταθερά ολοκλήρωσης που την γράφουμε
E0+ ΔΕ,
με έστω ΔΕ = KΔm C2, μετατροπή Μάζης κατά Δm,
αντιστοιχούσα σε ενέργεια ΔΕ.
Τότε θα ισχύει:
E1 = E0 + PC, Για την
απορρόφηση του φωτονίου.
E1 =ΔΕ + E0 + 1/2Pu, Για την απόκτηση Κ.Ε.
Αρα
ΔE = P(C - 1/2u)
Αν u=0 πρακτικά,
ΔΕ=PC=KΔmC2
ΔΕ= KΔmC2
με Κ διάφορο του μηδενός
Αν αυθαίρετα Κ=1
Τότε αυθαίρετα
ΔΕ=ΔmC2.
Δ' ΑΠΟΔΕΙΞΗ ΠΠ
ΓΙΑ ΤΗΝ ΑΝΑΓΚΑΙΟΤΗΤΑ ΔΥΝΑΜΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΜΑΖΗΣ
ΜΟΝΤEΡΝΑ
Πρωτότυπη απόδειξη αναγκαιότητας συνάρτησης ισοδυναμίας μαζης και ενέργειας απο τον ΠΠ.
Ίδιες προϋποθέσεις με την απόδειξη Γ'
Ισχύει γενικά στα πλαίσια της μοντέρνας φυσικής.
E
2 = Ε02 + P2C2Εφ = PC
Γενικά
E0=
E12
= E02 + Εφ2,
Μοντέρνα σχέση για τις ενέργειες.
E1
= E0
+ EΦ,Το
σώμα με αρχική ενέργεια Ε0
απορροφά φωτόνιο με ενέργεια
ΕΦ
=
PC. Οι ενέργειες αθροιζοντες σε E1
Οι δυο εξισώσεις, η μια
πυθαγορειος και η άλλη γραμμικη, ειναι αδύνατον να ισχύουν ταυτόχρονα.
Αναγκαστικά πρέπει να πούμε ότι, μετά την
αλληλεπίδραση, έχουμε ένα νέο σώμα, μέ νέα σταθερά ολοκλήρωσης που την γράφουμε
E0+ ΔΕ, με ΔΕ = KΔm C2, με μετατροπή Μάζης κατά
Δm, αντιστοιχούσα σε ενέργεια ΔΕ.
E12 = (E0+ ΔΕ)2 + Εφ2
E1
=[(K0 M0 + KΔm)2
C4 +
p2C2] 1/2
E1
=[(K0 M0
+ KΔm)2
C4 + P2C2]
½
E1 = K0 M0 C2 + PC
[K0 M0 C2 +
PC ]
2 = (K0
M0 +
KΔm)2
C4 + P2C2
K02 M02
C4 + P2C2
+2k0 M0 C2 PC =
K02 M02
C4 +
K2Δm2
C4 + 2k0 M0
KΔm
C4 + p2C2
2k0 M0 PC3
=k2Δm2C4+ 2k0 M0KΔm C4
PC=(KΔm+ K2Δm2/2k0 M0 )C2
= Εφ
Aν Δm<<M0, το σώμα πρακτικά ακίνητο
και όπως αναμένεται
Εφ = KΔmC2
Α' ΑΠΟΠΕΙΡΑ ΑΠΟΔΕΙΞΗΣ ΑΕ
Για την απόδειξη Ε = MC2
Annalen der Physik 17, 1905
Παρακάτω αντιπαραθέτουμε το πρωτότυπο από τις εκδόσεις Dover, "The Principle of Relativity", σελίδες 67-71, Standard Book # 486-60081-5.

Φωτ. 8,
έκδοσης Dover
σελ. 67
του τίτλου της εργασίας που επιχειρεί για
δεύτερη φορά να
αποδείξει την σχέση Ε = mc

Φωτ. 9 έκδοσης Dover σελ. 69, με τό λάθος τύπο για το φαινόμενο Doppler γιά το φώς, σύμφωνα με όλα τα σχετικά σημερινά βιβλία.

Φωτ. 10, έκδοσης Dover σελ. 70, με αυθαίρετους ορισμούς και υποθέσεις, στην αγωνιώδη προσπάθεια απόδειξης του λανθασμένου επιθυμητού, βλέπετε κείμενο παρακάτω.

Φωτ. 11, έκδοσης Dover σελ. 71, με το τελικό συμπέρασμα.
L*=L(1-ucosφ/c)/(1-u2/c2)1/2
Προτεινόμενος τύπος από τον ΑΕ για την ενέργεια
ενός φωτονίου, όπως την βλέπει ένας κινούμενος παρατηρητής (παρατηρητής
κινούμενος ως προς φωτονιο!!). Βλέπετε παραπάνω φωτοτυπία πρωτότυπου.
Σήμερα ξέρουμε L=hv, και ο παραπάνω τύπος συνεπάγεται το
λάθος Doppler για την συχνότητα v
φωτονίου που έχει διαστάσεις 1/t.
Κατά το πρωτότυπο, έστω ένα σώμα με αρχική Ενέργεια E0,
αντιστοίχως Η0 εκπέμπει δυο φωτόνια σε δυο
αντίθετες διευθύνσεις και με γωνία φ ως προς τους άξονες χ και αντιστοίχως Χ'
δυο παράλληλων και κινουμένων μεταξύ τους συστημάτων αναφοράς. E1,
Η1 είναι οι δυο ενέργειες αντίστοιχα μετά την εκπομπή,
στα δυο συστήματα (δεχόμεθα τον τύπο που προτείνει ο ΑΕ, έστω και αν συνεπάγεται
το λάθος φαινόμενο Doppler ή οχι):
E0 = E1 +1/2L +1/2L
H0 = H1 +1/2L(1-ucosφ/c)/(1-u2/c2) +1/2 L(1+ucosφ/c)/(1-u2/c2)1/2
= H1 + L/(1-u2/c2)1/2
H0– E0 – (H1– E1)=
L{1/(1-u2/c2)1/2
Κατά τους ορισμούς του κειμένου του ΑΕ:
ορισμός 1 ΑΕ: Α+K0 = H0– E0 = 1/2M0u2
ορισμός 2 ΑΕ: A+K1 = H1– E1= 1/2(M0-m0)u2
Άρα Κ0 - K1 = 1/2m0u2
Είναι Κ0 - K1 = H0– E0 – (H1–
E1)= 1/2Lu2/c2
Άρα 1/2Lu2/c2 = 1/2m0u2
L=m0c2
Αν km=m0,
Τότε
L=kmc2
και Γενικά
E=kmc2
ΣΤ' ΑΠΟΔΕΙΞΗ
Β' ΑΠΟΠΕΙΡΑ ΑΕ
Δημοσιευθείσα το 1906 στο
Ann. Phys. 20, 627-633, 1906
Δυσεύρετη Εργασία .
Παραθέτουμε την απόπειρα
από το
παρακάτω βιβλίο του A.P. French,
Καθηγητού Φυσικής στο ΜΙΤ.
Η απόπειρα συνίσταται από ένα “συλλογιστικό πείραμα” (gedanken - δηλαδή ένα πείραμα φανταστικό, μη εφικτό στην πραγματικότητα) επινόησης του Einstein το 1906, για το οποίο η προσδιδόμενη ορμή σε μία απορροφητική επιφάνεια θεωρείται E/C. O σκοπός αυτού του πειράματος είναι να δείξει ότι η ενέργεια συνδέεται με κάποια ισοδύναμη μάζα αδράνειας. Mε τον όρο “μάζα αδράνειας” εννοούμε το λόγο της γραμμικής ορμής προς την ταχύτητα. Θα υποθέσουμε ότι ένα ποσόν E ενέργειας ακτινοβολίας (μία δέσμη φωτονίων) εκπέμπεται από το ένα άκρο ενός κουτιού με μάζα M και μήκος L, το οποίο είναι απομονωμένο από το περιβάλλον του και αρχικά στάσιμο. H ακτινοβολία επιφέρει ορμή E/(ΚC), (με Κ οτιδήποτε), εφ’όσον δε η ολική ορμή του συστήματος παραμένει ίση προς το μηδέν, το κουτί πρέπει να αποκτήσει μία ορμή ίση προς -E/KC. Έτσι το κουτί ανακρούεται με ταχύτητα υ που δίδεται από τον τύπο:
υ =- E/ΚMC
Mετά από ελεύθερη κίνηση σε χρόνο Δt (= L/C πολύ κοντά, για υ << C), η ακτινοβολία διέρχεται μέσα από το άλλο άκρο του κουτιού και επιφέρει μία ώθηση, ίση και αντίθετη προς αυτήν που δόθηκε αρχικά, η οποία επαναφέρει το κουτί πάλι στην ηρεμία. Έτσι, το αποτέλεσμα είναι η μετακίνηση του κουτιού κατά μία απόσταση Δx:
Δx = u Δt = - EL/KMC2
Aλλά αυτό είναι μεμονωμένο σύστημα, οπότε είμαστε υποχρεωμένοι να δεχτούμε ότι το κέντρο μάζας του κουτιού μαζί με το περιεχόμενό του έχει μετακινηθεί. Έτσι δεχόμαστε ότι η ακτινοβολία έχει μεταφέρει μία ισοδύναμη μάζα m, έτσι ώστε:
mL + MΔx = 0
Συνδυάζοντας τις δύο τελευταίες εξισώσεις έχουμε:
m = E/(KC2) ή E = KmC2
Για τους πολλούς, ο
Einstein και η σχετικότητα συνοψίζονται συνήθως στο αποτέλεσμα με K =1.
Η απόπειρα έγκειται στο γεγονός, ότι ο
ΑΕ θεωρεί ότι η εκπομπή ή απορροφηση ενός φωτονίου από ένα σώμα, μεταφέρει ορμή
στο σώμα P= - E/C, αντί,
παραδείγματος χάριν της κλασσικής σχέσης της ορμής Ε=(1/2)PC=(1/2)mC2
που συνεπάγεται ορμή
P=-2E/C
και καταλήγει στο συμπέρασμα
E=mC2
Η απόπειρα είναι φανερή για το συμπέρασμα, διότι η χρήση της κλασσικής για την περίπτωση ορμής P=-2E/C,
μαθηματικά δίδει:
E=(1/2)mc2
Δηλαδή την κλασσική κινητική
ενέργεια του φωτονίου, αν υποθέταμε το φωτόνιο είχε μαζα m.
Θεωρώντας αυτό το φανταστικό πείραμα ορθο, αυτό που αποδεικνύεται είναι η ισχύς
των παραπάνω τύπων για την ισοδυναμία μάζης και ενέργειας, που συνδέουν την μάζα
του φωτονίου με την ισοδύναμο κινητική ενέργεια του φωτονίου, βάσει του νόμου
της κλασσικής μηχανικής του Νεύτωνα. Μήπως πρέπει να λάβουμε στα σοβαρά και την
περίπτωση αυτή που αντιστοιχεί σε Κ = 1/2;
Παρακάτω παραθέτουμε την πηγή των παραπάνω.

Φωτ. 12, εξωφύλλου του μετάφραση από τούς συμφοιτητές και φίλους μου- Παπαγιαννάκοπουλου και Μεταξά, βιβλίου Σχετικότητας του Καθ. Φυσικής του περιβόητου Μ.Ι.Τ. Α. P. French

Φωτ. 13, σελ. 15 από το βιβλίο του Α. P. French, γιά την τρίτη απόπειρα απόδειξης του ΑΕ για το αυθαίρετο Ε=mC2

Φωτ. 14, σελ. 16 από το βιβλίο του Α. P. French γιά την παραπάνω απόδειξη.
Συμπέρασμα και με την απόπειρα αυτή του ΑΕ, δεν γνωρίζουμε άλλη Μαθηματικά σωστή απόδειξη του E= mc
2 τουλάχιστον από τον ΑΕ.ΠΕΙΡΑΜΑΤΙΚΕΣ ΑΠΟΔΕΙΞΕΙΣ ΤΟΥ
E=kmc2
Η αντίδραση της βόμβας ουρανίου:
0
Φαίνεται να ισχυει με K συνηθως κοντα στο 1, οταν μια
βομβα U ριχνεται σε σημείο
x,y,z,t, με καταλληλο t.
Τότε, ελεγετο διακριτικα οτι πληροί την συνθηκη J, απο το Jesus, την εποχη των πυρηνικων δοκιμων, που δεν γνωριζαν τι
ακριβως συνεβαινε.
Αιθερικα σημερα θα λέγαμε, (ισοδυναμα, με βασει την ετερογενεια του χωροχρονου) :
Στον χρονο t, πρεπει να υπαρxει
αιθερικη πυλη για να εχουμε μεγαλο Κ, που θα προκαλέσει μεγάλη έκρηξη.
Εχουν παρατηρηθει εκρήξεις με Κ κοντα στο 3, και ισχύ τριπλάσια
από ότι αναμένατο.
Ας σημειωθει, οτι οι πυρηνικες δοκιμες στην ατμοσφαιρα απαγορευθηκαν με αμοιβαια και ακαριαία συμφωνια -την SALT Ι και ΙΙ- μεταξυ Σοβιετικης Ενωσης και ΗΠΑ, σε ενα περίεργο συντομο χρονο ρεκορ το 1956.
2.
Βιολογικες Πυρηνικες Αντιδρασεις:
Των
Louis Kervran και πολλών άλλων, απο την παλαιότερη
Βιβλιογραφία της Ιατρικης και Βιολογιας, πχ:
11 Na23 + 8O16 = 19K39
ειναι η κυρια πυρηνικη αντιδραση για την συντηρηση της ζωης.
Φαινεται να ισχυει για μετριο Κ<1
3.
Οι παρακάτω βιολογικές πυρηνικές αντιδράσεις:
19K39 + 1H1 = 20Ca40
14Si28 + 6C12 = 20Ca40
είναι πυρηνικες αντιδρασεις παραγωγης Ca στα ζωα και ανθρωπους.
Φαινεται να ισχυουν με Κ παρα πολυ μικρο.
Οι αντιδράσεις αυτές ανά Mol Ca είναι ισοδύναμες - της αυτής τάξης ενέργειας της βόμβας ουρανίου ανά Mol U, διά Κ=1 !
4.
Ψυχρη Πυρηνικη Συντηξη.
Ποικιλες πυρηνικες αντιδρασεις, υπο ευρεια λογοκρισια, κυριως σε διαταξεις
ηλεκτρολυσης, με διαφορα σχετικα Κ.
5.
Παραδοσιακη Αλχημεια, υπο αποσιωπηση-εξαφανηση:
είναι κυρίως μεταστοιχειώσεις Μετάλλων (παραβαλε
ορθογραφια-ετοιμολογια με το "Μεταλλαζω-Μεταλλασομενο"). Αντιδρασεις που
γινονται με πολυ μικρο Κ και που γίνονται σε συγκεκριμενες και καταλληλες
χρονοπυλες, αντιπαράβαλε βομβα U παραπανω. Οι χρονοπυλες
ήταν απο
τα καλά και ευκολα φυλασσόμενα μυστικα των αλχημιστων.
Ποτέ οι αλχημιστές δεν έγραφαν τον χημικό τύπο αντίδρασης μαζί με την
απαιτούμενη χρονοπύλη στις ίδιες σημειώσεις.
6.
Τόποι Ασκληπιείων:
ήτανε τόποι με εξαιρετικές θεραπευτικές
ιδιότητες.
Κατα την άποψη του συγγραφέα τα Ασκληπιεία είναι τόποι που το Κ των Βιολογικών Πυρηνικών Αντιδράσεων λαμβάνει εξαιρετικά χαμηλές τιμές, διευκολύνοντας την Βιολογία των Ασθενών.

Φωτ. 15, από το εξώφυλλο του Ιατρικού Οδηγού "ΠΑΠΥΡΟΣ"
© 1968
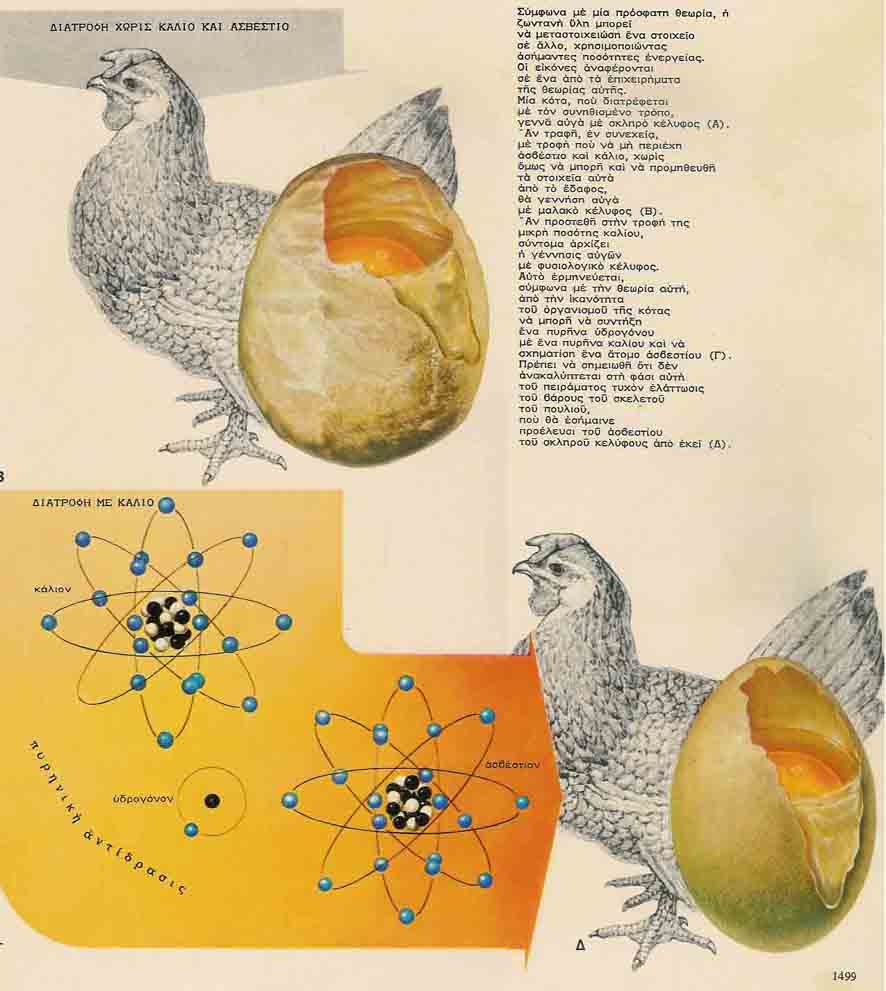
Φωτ. 16, με Διαπίστωση
του Ιατρικού Οδηγού "ΠΑΠΥΡΟΣ"
© 1968
ότι το Κάλιο μετατρέπεται σε
Ασβέστιο Πυρηνικά.
Ανεξάρτητες και πρόσφατες επιβεβαιώσεις των ανωτέρω :
"H περίφημη εξίσωση Ε=mc2 δεν ισχύει ......... "
Σημειωτέον ότι στο Πανεπιστήμιο του Stanford επεξεργάζονται τα πειραματικά δεδομένα του πειράματος Gravity Probe II - το οποίο θα επιβεβαίωνε ή θα διέψευδε τη Σχετικότητα - τα οποία δεδομένα δεν έχουν ανακοινώσει, και τα οποία απαράδεκτα καθυστερούν να δημοσιευθούν παρά την κατηγορηματική υπόσχεση για την άμεση και έγκαιρη δημοσιοποίηση των on-line όπως αυτά θα ελαμβάνοντο από τον δορυφόρο….
Μήπως η παραπάνω δήλωση για την μη γενική ισχύ του Ε=mc2 αποτελεί προοίμιο και εισαγωγή για μια γενικότερη διάψευση της θεωρίας της Σχετικότητας που αποδεικνύεται από τα αποτελέσματα του Gravity Probe II τα οποία προς το παρόν κρατούνται μυστικά από την Επιστημονική Κοινότητα….
Επειδή στη βασική εργασία του ΑΕ του 1905,
αντικανονικά, δεν εδώθηκε καμία αναφορά, ας δούμε από άλλες πηγές, από τι
παρορμήθηκε και
τι αληθινά εγνώριζε ο ΑΕ πριν τις δημοσιεύσεις του. Διαβάζετε
παρακάτω.
Πραγματικά, βασική πηγή παρόρμησης ήταν τα μεγάλα άλυτα προβλήματα του Ηλεκτρομαγνητισμού, όπως τα έθετε ο Lorentz, και όχι το ακαδημαϊκό ενδιαφέρον για την σταθερότητα το φωτός. Τό σημαντικότατο δε είναι τα ίδια αυτά άλυτα προβλήματα εξακολουθούν να είναι άλυτα και σήμερα.
Πράγματι, η περίφημη και βασική ηλεκτροδυναμική
δύναμη του Lorentz με τα άπειρα παράδοξά της, εξακολουθεί
να είναι το μεγάλο άλυτο αίνιγμα-μυστικό της φύσης για όλους τους φυσικούς του
κόσμου σήμερα.
ΠΑΝΑΓΙΩΤΗΣ ΠΑΠΠΑΣ

Φωτ. 17 από το Περισκόπιο της Επιστήμης τεύχος 77, σελ 47

Φωτ. 18 από το Περισκόπιο της Επιστήμης τεύχος 77, σελ 48

Φωτ. 19 από το Περισκόπιο της Επιστήμης τεύχος 77, σελ 49

Φωτ. 20, από το Περισκόπιο της Επιστήμης τεύχος 77, σελ 50
ΟΡΓΑΝΩΣΗ
βλέπετε και
www.papimi.gr
click
HELLENIC VERSION
Click here for E = kmc2 in English
Γιά άμεση κριτική,
συζήτηση, δημοσίευση:
![]()
![]()
info@papimi.gr isnot functional